백준 11660 c++ -[PlusUltraCode]

 

https://cocoon1787.tistory.com/377 그림 출처

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

[필자 사고]

 

전형적인 구간 합 알고리즘을 사용하는 문제이다.

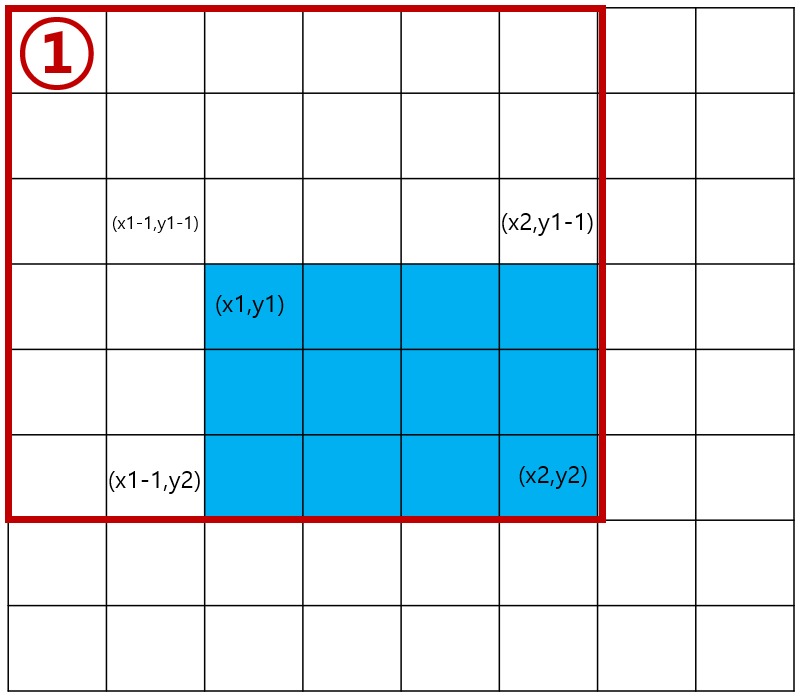
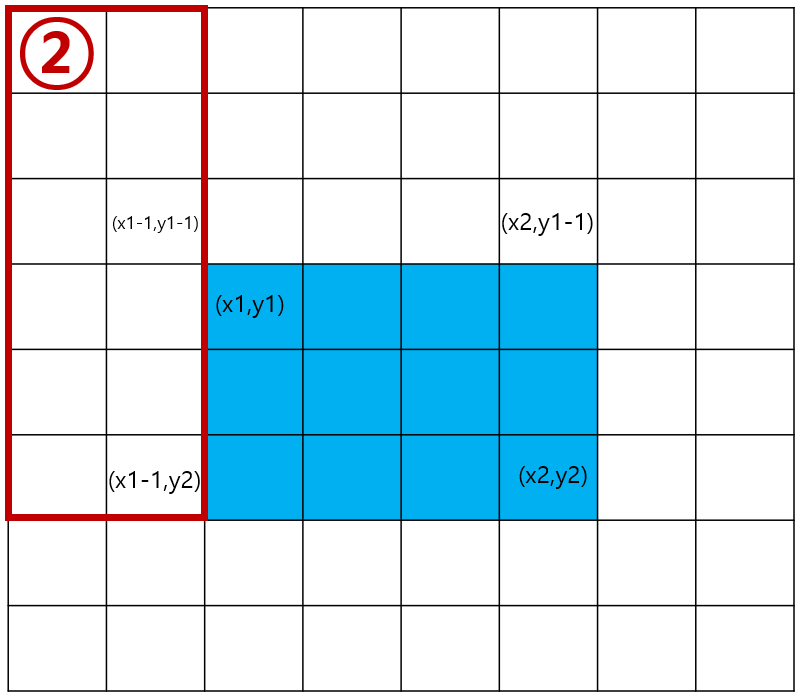
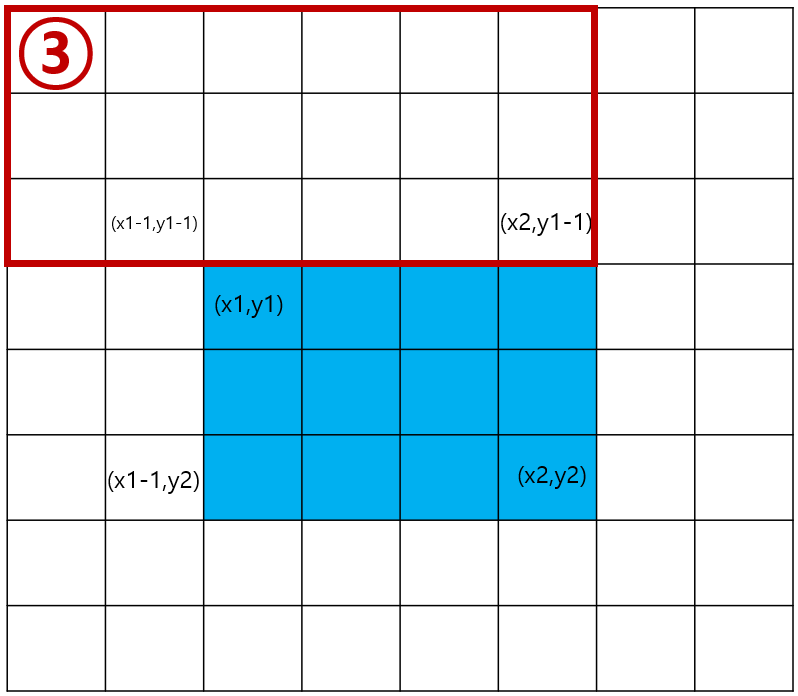
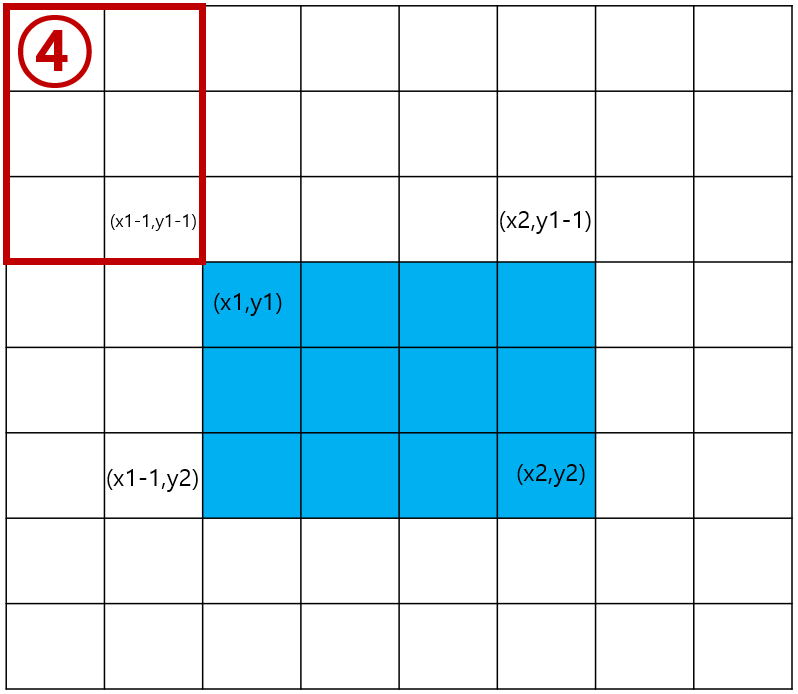
2차원 평면에서 구간합 알고리즘을 사용하기 위해서는 위의 그림을 통해 이해 해야 된다.

 

기본적으로 S라는 구간합을 만드는 배열이든 그 배열에서 범위 내 합을 구하든 똑같은 원리가 적용된다.

 

1. 1번 그림에서 2번과 3번 그림을 빼고 4번그림은 두번 빼진거므로 한번 더해주면된다.

2.  S[i][k]= 2번 빼고 3번빼고 4번 더한다.

 

[소스 코드]

 

 

 

 

#include <iostream>
#include <vector>
#include <cstring>
#include <string>

using namespace std;

int N, M;

vector<vector<int>> Arr;
vector<vector<int>> S;

void Input() {
	cin >> N >> M;
	
	Arr.resize(N + 1);
	S.resize(N + 1); 
	for (int i = 0; i <= N; i++) {
		Arr[i].resize(N + 1);
		S[i].resize(N + 1);
	}
	for (int i = 1; i <= N; i++) {
		for (int k = 1; k <= N; k++) {
			cin >> Arr[i][k];
		}
	}

	for (int i = 1; i <= N; i++) {
		for (int k = 1; k <= N; k++) {
			S[i][k] = S[i - 1][k] + S[i][k - 1] + Arr[i][k] - S[i - 1][k - 1];

		}
	}
	
}

void Solve() {
	for (int i = 0; i < M; i++) {
		int x1, y1, x2, y2;
		cin >> x1 >> y1 >> x2 >> y2;
		cout << S[x2][y2] - S[x2][y1 - 1] - S[x1 - 1][y2]+S[x1-1][y1-1] << '\n';
	}
}

int main(void) {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	Input();
	Solve();
}