https://www.acmicpc.net/problem/18135
[필자 사고]
이 문제는 세그먼트 자료구조를 이용하여 푸는 문제이다.
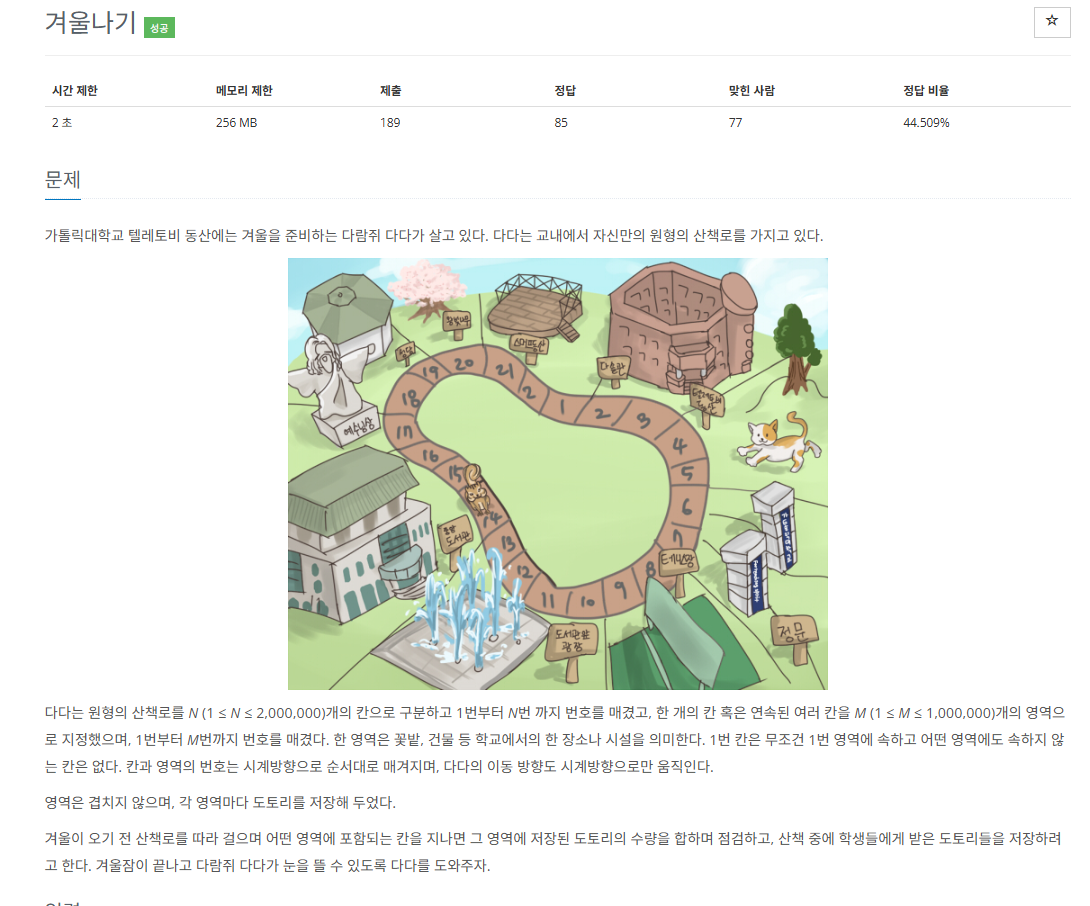
이 문제만의 특이점은 경로가 원형으로 되어 있다는 점이다.
또한 특정 범위에 들어가면 갯수를 얻는 시스템이다 보니 좌표 압축을 해야 된다.
이 두가지 점만 신경쓰면 해결할 수 있다.
[코드 해설]
1. 세그먼트 트리 초기화 (Init_Tree 함수)
Init_Tree 함수는 세그먼트 트리를 초기화합니다. 배열 arr의 값을 기반으로 세그먼트 트리를 구성하며, 다음과 같은 방식으로 작동합니다:
- 기저 사례: start와 end가 같으면 리프 노드에 arr[start] 값을 설정합니다.
- 재귀 호출: 현재 구간을 절반으로 나누어 왼쪽과 오른쪽 자식 노드를 초기화한 후, 두 자식 노드의 합을 부모 노드에 저장합니다.
2. Lazy Propagation 처리 (Propagation 함수)
Lazy propagation은 세그먼트 트리의 업데이트를 효율적으로 수행하기 위한 기법입니다. Propagation 함수는 다음을 수행합니다:
- 현재 노드에 저장된 lazy 값을 반영하고, 자식 노드로 값을 전달합니다.
- 이를 통해 모든 업데이트가 즉시 반영되지 않고, 필요할 때만 계산하도록 최적화합니다.
3. 구간 합 계산 (Query 함수)
Query 함수는 사용자가 원하는 구간 [left, right]에 대해 합산 결과를 반환합니다:
- Propagation 호출: 먼저 lazy 값을 반영합니다.
- 기저 사례:
- 현재 노드가 완전히 범위 안에 있으면 결과를 반환합니다.
- 현재 노드가 범위를 벗어나면 0을 반환합니다.
- 재귀 호출: 구간을 왼쪽과 오른쪽으로 나누어 결과를 합산합니다.
4. 구간 업데이트 (Update 함수)
Update 함수는 사용자가 지정한 구간 [left, right]에 값을 더합니다:
- Propagation 호출: 먼저 lazy 값을 반영합니다.
- 기저 사례:
- 현재 노드가 완전히 범위 안에 있으면 lazy 값을 설정하고 종료합니다.
- 현재 노드가 범위를 벗어나면 작업을 종료합니다.
- 재귀 호출: 구간을 왼쪽과 오른쪽으로 나누어 업데이트를 수행합니다.
5. 입력 처리 (Input 함수)
Input 함수는 입력 데이터를 처리하고 초기화를 수행합니다:
- 기본 입력:
- 정수 N과 M을 입력받고, 세그먼트 트리(tree)와 lazy 배열(lazy)의 크기를 조정합니다.
- arr 배열과 num 배열을 초기화합니다.
- 범위 입력:
- M개의 범위 [a, b]와 값 c를 입력받아 arr와 num 배열을 구성합니다.
- num[k]는 범위의 인덱스를, arr는 해당 값 c를 저장합니다.
- 세그먼트 트리 초기화:
- 입력받은 데이터를 바탕으로 세그먼트 트리를 초기화합니다.
- 명령 처리:
- 명령 a에 따라 동작을 수행합니다:
- a == 1: [b, c] 범위의 합을 계산하여 출력합니다.
- a == 2: [b, c] 범위에 값 d를 더합니다.
- 범위가 순환하는 경우(b > c), 두 구간으로 나누어 처리합니다.
- 명령 a에 따라 동작을 수행합니다:
[소스 코드]
#include <iostream>
#include <vector>
#define ll long long
using namespace std;
int N, M;
vector<ll> tree;
vector<ll> lazy;
vector<int> num;
vector<ll> arr;
void Propagation(int node, int start, int end) {
if (lazy[node] != 0) {
tree[node] = tree[node] + lazy[node] * (end - start + 1);
if (start != end) {
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
}
ll Query(int node, int start, int end, int left, int right) {
Propagation(node, start, end);
if (left > end || right < start) return 0;
if (left <= start && right >= end) return tree[node];
int mid = (start + end) / 2;
long long l = Query(node * 2, start, mid, left, right);
long long r = Query(node * 2 + 1, mid + 1, end, left, right);
return l + r;
}
void Update(int node, int start, int end, int left, int right, long long value) {
Propagation(node, start, end);
if (start > right || end < left) return;
if (start >= left && end <= right) {
tree[node] = tree[node] + value * (end - start + 1);
if (start != end) {
lazy[node * 2] += value;
lazy[node * 2 + 1] += value;
}
return;
}
int mid = (end + start) / 2;
Update(node * 2, start, mid, left, right, value);
Update(node * 2 + 1, mid + 1, end, left, right, value);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
void Init_Tree(int node, int start, int end) {
if (start == end) {
tree[node] = arr[start];
return;
}
int mid = (start + end) / 2;
Init_Tree(node * 2, start, mid);
Init_Tree(node * 2 + 1, mid + 1, end);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
void Input() {
cin >> N >> M;
tree.resize(N * 4);
lazy.resize(N * 4);
arr.resize(1000001);
num.resize(2000001);
for (int i = 0; i < M; i++) {
int a, b, c;
cin >> a >> b >> c;
for (int k = a; k <= b; k++) {
num[k - 1] = i;
arr[i] = c;
}
}
Init_Tree(1, 0, M - 1);
while (1) {
int a, b, c, d;
cin >> a >> b >> c;
if (a == 0)break;
else if (a == 1) {
ll ret = 0;
if (b <= c) {
ret += Query(1, 0, M - 1, num[b - 1], num[c - 1]);
}
else {
ret += Query(1, 0, M - 1, num[b - 1], M - 1);
ret += Query(1, 0, M - 1, 0, num[c - 1]);
}
cout << ret << "\n";
}
else {
cin >> d;
if (b <= c) {
Update(1, 0, M - 1, num[b - 1], num[c - 1], d);
}
else {
Update(1, 0, M - 1, num[b - 1], M - 1, d);
Update(1, 0, M - 1, 0, num[c - 1], d);
}
}
}
}
int main(void) {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
Input();
}'백준 > 자료구조' 카테고리의 다른 글
| 백준 1406 c++ "에디터" -PlusUltraCode- (0) | 2025.05.27 |
|---|---|
| 백준 17353 c++ "하늘에서 떨어지는 1, 2, ..., R-L+1개의 별" -PlusUltraCode- (0) | 2025.01.20 |
| 백준 15899 c++ "트리와 색깔" -PlusUltraCode- (0) | 2025.01.19 |
| 백준 2820 c++ "자동차 공장" -PlusUltraCode- (0) | 2025.01.18 |
| 백준 15967 c++ "에바쿰" -PlusUltraCode- (0) | 2025.01.17 |



